איך ללמוד רקורסיה באופן אינטואיטיבי

בשביל ללמוד רקורסיה, צריך ללמוד רקורסיה! או איך ללמוד רקורסיה the intuitive way 🙂.

פונקציה רקורסיבית היא פונקציה שקוראת לעצמה בתוך עצמה (ושכולם כבר הפנימו כנראה). אבל עדיין יש אלמנטים עמומים שמבלבלים אנשים ברקורסיה (ובצדק).

הדבר הראשון שמבלבל אנשים הוא איך קוראים לפונקציה בתוך עצמה, כשלא סיימנו עדיין את הפונקציה. הדבר השני, הוא איך ההיגיון מאחורי הקלעים עובד, שפולט את התשובה הנכונה כמו קסם.

הסיבה שלקרוא לפונקציה בתוך עצמה “עובד”, הוא בגלל שכל קריאה לפונקציה נשמרת בזיכרון ב-stack (מחסנית), אשר עובדת לפי אחרון נכנס, ראשון יוצא. לדוגמה, אם נריץ את האלגוריתם הבא:

func(n = 4): if n == 0 return func(n-1) print(n)

קודם כל יודפס 1, אח"כ 2, 3 ואז 4. זה בגלל שהקריאות נשמרות במחסנית לפי הסדר הבא: קודם נכנס למחסנית func(4), אחריו func(3)…עד 0, הקריאה העליונה במחסנית. כשמגיעים לתנאי העצירה (0), מפסיקים לשמור קריאות במחסנית ומתחילים לעבור לשורת ההדפסה print בכל אחת מהקריאות מהסוף להתחלה במחסנית: מדפיסים 1, ואז 2 וכן הלאה.

קטע מעניין, הוא שעדיין אפשר להגיע ל-stackoverflow גם מבלי להשתמש במשפט הקסם “בלי תנאי עצירה”, שכן אם נציב מספר גדול כמו 10000, האלגוריתם עדיין יקרוס מ-stackoverflow בגלל השימוש הכבד במחסנית (צריך לשמור n קריאות במחסנית).

לעומת זאת, אם נחליף את הסדר של ה- print:

func(n = 4): if n == 0 return print(n) func(n-1)

ההדפסה תהיה הפוכה: התוצאה שנקבל היא 4, אחריו 3, 2, ואז 1. הפונקציה מדפיסה את המספר n, וקוראת לעצמה שוב עם n-1. ברגע שהגענו לתנאי העצירה n=0, אין עוד מה לעשות והקריאות חוזרות אחת אחרי השניה מהסוף להתחלה ללא קריאה לפעולות נוספות. אלגוריתם כזה נקרא tail recursion.

ההגדרה המילולית ל-tail recursion היא “הפעולה האחרונה של הפונקציה היא הקריאה לפונקציה עצמה”, כלומר אין עוד שורות או חישובים נוספים שעליה לבצע והיא מחזירה את התוצאה הסופית (אם יש מה להחזיר, לא במקרה שלנו). אלגוריתם שמשתמש ב-tail recursion יכול להיות לפעמים יעיל יותר מרקורסיה רגילה, שכן יש קומפיילרים המסוגלים לייעל את השימוש במחסנית (כלומר מתנהג כמו מימוש איטרטיבי).

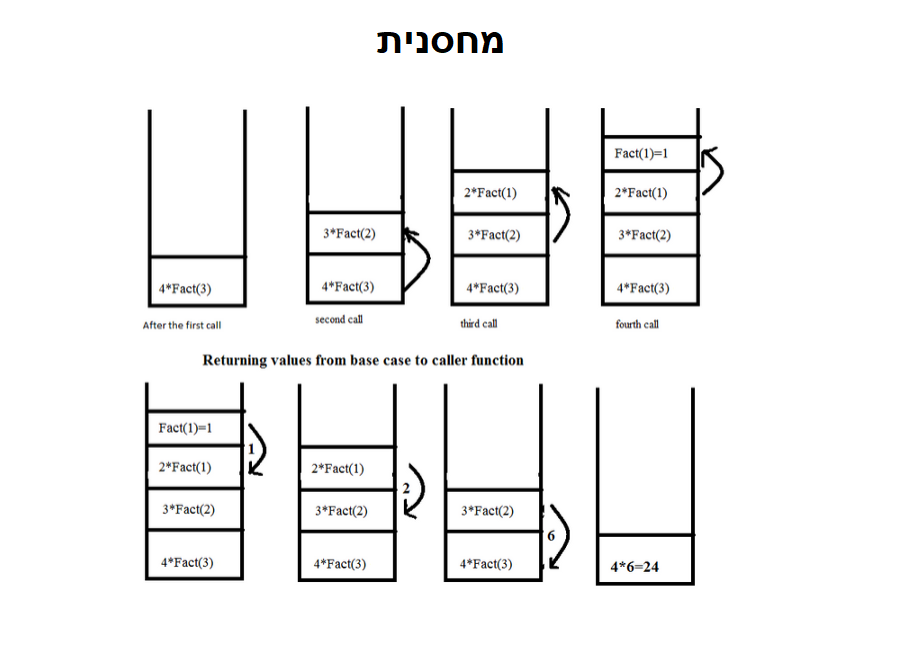
באלגוריתמים בהם צריך להחזיר תוצאה, כמו למשל בפונקציה רקורסיבית לחישוב עצרת (כאשר n = 4), הרעיון עובד בצורה דומה: fact(n = 4) if n == 1 return 1 return n*fact(n-1)

הקריאה הראשונה שנכנסת למחסנית הוא fact4, והיא אומרת “תן לי את התוצאה של fact3 ואני אתן לך את התוצאה של 4!. אותו דבר ל-fact3 עד שמגיעים ל n = 1, שבמקרה מחזיר 1 כתנאי עצירה. ואז מלמעלה למטה:

fact(1) = 1 fact (2) = 2 * fact(1) = 21 fact(3) = 3 * fact(2) = 32 fact(4) = 4 * fact(3) = 4*6 = 24

אלגוריתם של tail recursion ייראה כך:

facTail(n = 4, results = 1): if(n == 1) return results return facTail(n-1, results * n)

הפעולה האחרונה היא קריאה רקורסיבית, והפונקציה מעדכנת את הפרמטר results עד התנאי עצירה, מחזירה את הערך הסופי ומעיפה את כל הקריאות מהמחסנית אחד אחד.

בגלל השימוש הנדיב שלה במחסנית, רקורסיה (לפחות רגילה) תהיה איטית יותר מאלגוריתם איטרטיבי, ולכן ברוב המקרים התירוץ להשתמש באלגוריתם רקורסיבי יהיה בהתאם לאינטואיטיביות של המימוש.

בדר"כ האלגוריתמים האינטואיטיביים למימוש רקורסיבי הם במעבר על עצים, או מימושים של בעיות divide and conquer או במילים ישראליות- לפוצץ את הבעיה לחתיכות קטנות ולפתור. האלגוריתם לפתרון של tower of hanoi היא דוגמה ממש נפלאה לאיך אלגוריתם איטרטיבי ומסובך נחתך למס’ שורות מצומצם במימוש רקורסיבי.

הרעיון המרכזי שצריך להפנים בפונקציה רקורסיבית רגילה, היא איך נשמרות הקריאות במחסנית, ולעבוד מלמעלה למטה- ואז הרבה יותר קל להבין את ההגיון מאחורי האלגוריתם. ב- tail recursion צריך להפנים שבסה"כ מעדכנים כל פעם פרמטר(ים) ועובדים איתו מהגדול לקטן עד שבסוף מחזירים אותו.