כדי למדוד מהירות (פוטנציאל) אלגוריתמי כלשהיא, אנחנו נאלצים לבודד את המשתנים אשר מפריעים לנו למדוד את הפוטנציאל הטהור של האלגוריתם, כמו לבודד את המכונה מהמשוואה. איננו רוצים שאלגוריתם יהיה מהיר יותר כי יש לך את ה- AMD Ryzen החדש. בשביל זה יש לנו את הסיבוכיות- המודדת את כמות האופרציות שאלגוריתם מבצע, וכך נוכל להעריך גם את הפוטנציאל.
חיפוש בינארי הוא עוד אלגוריתם שנולד מתוך הרצון לחתוך כמה שיותר את כמות האופרציות בזמן חיפוש, והקונספט שלו דומה לחיפוש בספרי דפי זהב שפעם היה לכולנו. במקום לחפש איבר אחד אחרי השני, אנחנו חותכים את החיפוש ספציפית לאות שבה מתחיל השם שאנחנו מחפשים. זה כל כך אפקטיבי, שאנחנו יכולים למצוא שם של אדם תוך כמה שניות, מאשר אפילו כמה שעות.
יש לציין, שאי אפשר לבצע חיפוש בינארי עם הרשימה לא מסודרת. לא נוכל לחפש לפי אות אם האותיות לא מסודרת לפי ה- א’ ב'.
המשמעות של בינארי, אגב, פירושו יחס בין 2 פרטים. 0 או 1. זה או זה. פה או שם. ומכאן השם של חיפוש בינארי-אם לא פה אז אולי שם.
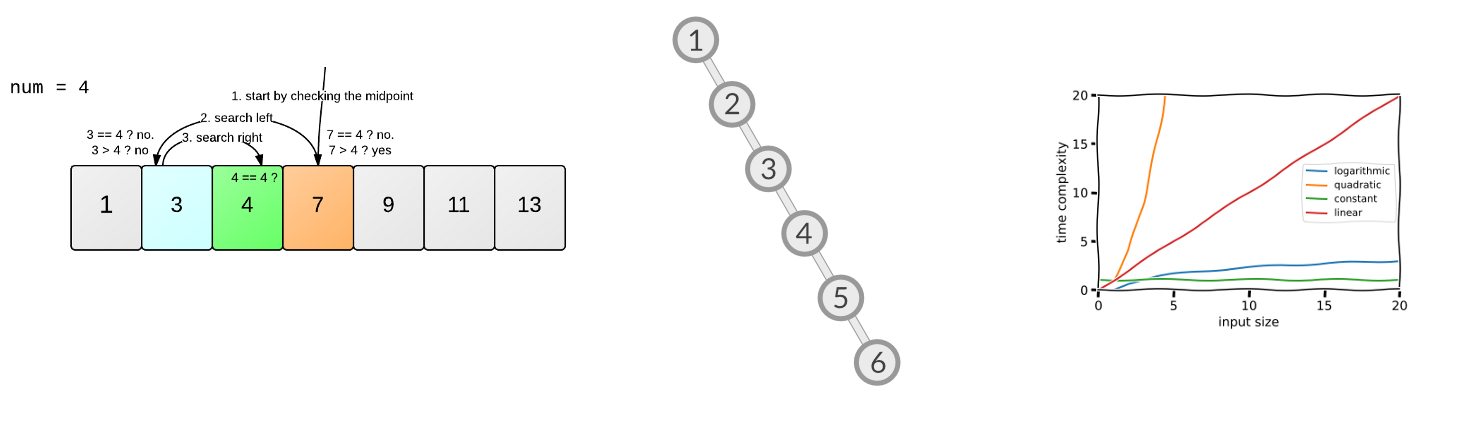
אז הקונספט של חיפוש בינארי הוא דיי קליל. ניקח מערך מספרים ממויין, ונחפש ספרה כלשהיא. נתחיל מהאמצע- אם הספרה לא שווה, האם היא גדולה מן הספרה האמצעית? אם כן, נחתוך את הרשימה בחצי ונתחיל שוב, וכך הלאה. המעבר של “לחתוך בחצי” את המערך נותן לנו סיבוכיות של logn, במקום סיבוכיות של n, בה נצטרך לעבור איבר איבר במערך (דמיינו מעבר לפי שם שם בדפי זהב לפי הסדר של הא’ ב’).
הפונקציה ’log’ היא שיטה נעימה (או פחות?) יותר לשאלה: הבסיס בחזקת מה, ייתן לי את המספר x? בדר"כ כשרואים ‘רק’ את המילה log, מתכוונים לבסיס 2. כלומר, כמות הפעמים שנחתוך את המערך עד למציאת האיבר שלנו, היא במקרה הכי גרוע פשוט החזקה. אם המערך שלנו הוא באורך 8, ייקח לנו במקסימום 3 פעמים שנצטרך לחתוך ולמצוא את האיבר שלנו.
זה נהיה קריטי כשהמערך גדל מעריכית, אבל כמות האופרציות נשארת כפונקציה לוגריתמית.
ומכאן אפשר לשאול, יש לנו חיפוש בינארי- למה צריך עץ בינארי? עץ בינארי גם מאפשר לנו חיפוש בlogn, אבל כמובן רק אם הוא עץ מאוזן (כדוגמת עצי AVL, אדום שחור). אם העץ אינו מאוזן, הוא יכול לתת לנו חיפוש ב- logn, אבל החיפוש יכול להיות לינארי (בהתאם לכמות האיברים, n). לעומת זאת אם הוא מאוזן, הוא מבטיח לנו תמיד חיפוש בlogn.
היתרון שיש לעצים בינארים מאוזנים על פני חיפוש בינארי, הוא דווקא בהכנסה וההוצאה (insert, remove). בעצים בינארים מאוזנים גם ההכנסות וההוצאות נשארים logn (על אף שהם צריכים לאזן את עצמם), בזמן שבמערכים ההכנסה וההוצאה היא לינארית, בהתאם ל- n ולמיקום במערך שיש להוסיפה.
לכן, המימוש של עצים בינארים יהיה מהיר יותר למקרים בהם לא רק יש צורך לחפש, אלא לבצע מניפולאציה כבדה על האיברים במערך.